2023 7급 국가직 전자회로 1번 R g R_g R g 0 0 0
R L = 12 − 8 0.5 = 16 k Ω \begin{equation} \begin{split} R_L&=\frac{12-8}{0.5}\\ &=16\text{ k}\Omega \end{split} \end{equation} R L = 0.5 12 − 8 = 16 k Ω 이므로 답은 3번 이다.
2번 τ = R C = 300 × 1 0 − 6 = 3 × 1 0 − 4 \begin{equation} \begin{split} \tau&=RC\\ &=300\times 10^{-6}\\ &=3\times 10^{-4} \end{split} \end{equation} τ = RC = 300 × 1 0 − 6 = 3 × 1 0 − 4 이다. 한편 반송파의 주기는 주파수의 역수이므로
T s = 1 0 − 4 T_s=10^{-4} T s = 1 0 − 4 이다. 그러므로 시정수는 반송파 주기의 3배이고 답은 1번 이다.
3번 그렇다. 그렇다. 양호도는 저장전력 소모전력 = ω L R \frac{\text{저장전력}}{\text{소모전력}}=\frac{\omega L}{R} 소모전력 저장전력 = R ω L 3번 보기의 설명에 의해 옳지 않다. 따라서 답은 4번 이다.
4번 우선 A = 0 A=0 A = 0 Y = 0 Y=0 Y = 0 A = 1 A=1 A = 1 B = C = 0 B=C=0 B = C = 0 Y = 0 Y=0 Y = 0
이므로 답은 3번 이다.
5번 A = 0 A=0 A = 0 Q 1 Q_1 Q 1 Q 2 Q_2 Q 2 F = 1 F=1 F = 1 A = 1 A=1 A = 1 Q 2 Q_2 Q 2 B = 0 B=0 B = 0 Q 3 Q_3 Q 3 F = 0 F=0 F = 0 3번 이다.
6번 V i V_i V i
15 × 1 6.8 + 1 ≈ 15 ≈ 1.92 V 15\times\frac{1}{6.8+1}\approx 15\approx 1.92\text{ V} 15 × 6.8 + 1 1 ≈ 15 ≈ 1.92 V 이다. 그러다 V i = 1.92 + 0.7 = 2.62 V_i=1.92+0.7=2.62 V i = 1.92 + 0.7 = 2.62
V i − V o 1 = V o − 0.7 − 15 6.8 + V o − 0.7 1 ≈ V o − 0.7 − 15 7 + V o − 0.7 ⇒ 7 V i − 7 V o ≈ V o − 0.7 − 15 + 7 V o − 4.9 ≈ V 0 − 1 − 15 + 7 V o − 5 ⇒ 7 V i − 7 V o ≈ 8 V o − 21 ⇒ 15 V o = 7 V i + 21 V o ≈ 0.5 V i + 1.4 \begin{equation} \begin{split} \frac{V_i-V_o}{1}&=\frac{V_o-0.7-15}{6.8}+\frac{V_o-0.7}{1}\\ &\approx \frac{V_o-0.7-15}{7}+V_o-0.7\\ \Rightarrow 7V_i-7V_o&\approx V_o-0.7-15+7V_o-4.9\\ &\approx V_0-1-15+7V_o-5\\ \Rightarrow 7V_i-7V_o&\approx 8V_o-21\\ \Rightarrow 15V_o&=7V_i+21\\ V_o&\approx 0.5V_i+1.4 \end{split} \end{equation} 1 V i − V o ⇒ 7 V i − 7 V o ⇒ 7 V i − 7 V o ⇒ 15 V o V o = 6.8 V o − 0.7 − 15 + 1 V o − 0.7 ≈ 7 V o − 0.7 − 15 + V o − 0.7 ≈ V o − 0.7 − 15 + 7 V o − 4.9 ≈ V 0 − 1 − 15 + 7 V o − 5 ≈ 8 V o − 21 = 7 V i + 21 ≈ 0.5 V i + 1.4 이다. 따라서 입력이 +20 V일 때 출력은 약 11.4 V가 나온다.(보다 정확히는 10.7 V 정도이다.)
그러므로 답은 없다.
시뮬레이션 결과는 다음과 같다.
(정정을 도와주신 중관소 꿈나무님께 감사드립니다.)
7번 +단의 전압을 V + V_+ V +
V + − 3 + V + − 1 + V + − 8 = 0 ⇒ V + = 4 V \begin{equation} \begin{split} V_+-3+V_+-1+V_+-8&=0\\ \Rightarrow V_+=4\text{ V} \end{split} \end{equation} V + − 3 + V + − 1 + V + − 8 ⇒ V + = 4 V = 0 이다.
비반전 증폭기이므로
V o = ( 1 + 20 10 ) × 4 = 12 V V_o=\left(1+\frac{20}{10}\right)\times 4=12\text{ V} V o = ( 1 + 10 20 ) × 4 = 12 V 이고 답은 4번 이다.
8번 제대로 풀자면 임피던스들을 다 구해서 풀어야겠으나, 출력의 주파수 응답으로부터 식의 형태를 추론해보자.
s = 0 s=0 s = 0 C 1 C_1 C 1 s = ∞ s=\infty s = ∞ C 2 C_2 C 2 s R C sRC s RC s R C \frac{s}{RC} RC s 4번 이 답이다.
9번 공진 상태일 때 커패시터와 인덕터는 서로의 효과를 상쇄시킨다.
총 컨덕턴스를 구해보면
G ( ω ) = j 0.1 ω + 1 5 + 1 2 + j 2 ω = j 0.1 ω + 1 5 + 2 − j 2 ω 4 + 4 ω 2 = j 0.1 ω + 1 5 + 1 − j ω 2 + 2 ω 2 \begin{equation} \begin{split} G(\omega)&=j0.1\omega+\frac{1}{5}+\frac{1}{2+j2\omega}\\ &=j0.1\omega+\frac{1}{5}+\frac{2-j2\omega}{4+4\omega^2}\\ &=j0.1\omega+\frac{1}{5}+\frac{1-j\omega}{2+2\omega^2} \end{split} \end{equation} G ( ω ) = j 0.1 ω + 5 1 + 2 + j 2 ω 1 = j 0.1 ω + 5 1 + 4 + 4 ω 2 2 − j 2 ω = j 0.1 ω + 5 1 + 2 + 2 ω 2 1 − jω 이다. 공진일 때 허수부가 0이므로
0.1 ω − ω 2 + 2 ω 2 = 0 ⇒ 2 + 2 ω 2 = 10 ⇒ ω 2 = 4 ⇒ ω = 2 \begin{equation} \begin{split} 0.1\omega-\frac{\omega}{2+2\omega^2}&=0\\ \Rightarrow 2+2\omega^2&=10\\ \Rightarrow \omega^2&=4\\ \Rightarrow \omega&=2 \end{split} \end{equation} 0.1 ω − 2 + 2 ω 2 ω ⇒ 2 + 2 ω 2 ⇒ ω 2 ⇒ ω = 0 = 10 = 4 = 2 이고 답은 2번 이다. (오타 알려주신 통신해보자님 감사합니다.)
10번 모두 네거티브 피드백이 있으므로 가상 도통 상태이다. 아래 그림을 보자.
V 3 − V 2 = V 2 − V a + V 2 − V 1 V a − V 1 = V 1 − V o + V 1 − V 2 ⇒ V 3 − V 2 = V 2 − ( 3 V 1 − V 2 − V o ) + V 2 − V 1 ⇒ V 3 − V 2 = − 4 V 1 + 3 V 2 + V o ⇒ V o = 4 V 1 − 4 V 2 + V 3 \begin{equation} \begin{split} V_3-V_2&=V_2-V_a+V_2-V_1\\ V_a-V_1&=V_1-V_o+V_1-V_2\\ \Rightarrow V_3-V_2&=V_2-(3V_1-V_2-V_o)+V_2-V_1\\ \Rightarrow V_3-V_2&=-4V_1+3V_2+V_o\\ \Rightarrow V_o&=4V_1-4V_2+V_3 \end{split} \end{equation} V 3 − V 2 V a − V 1 ⇒ V 3 − V 2 ⇒ V 3 − V 2 ⇒ V o = V 2 − V a + V 2 − V 1 = V 1 − V o + V 1 − V 2 = V 2 − ( 3 V 1 − V 2 − V o ) + V 2 − V 1 = − 4 V 1 + 3 V 2 + V o = 4 V 1 − 4 V 2 + V 3 이므로 답은 3번 이다.
11번 총 전압 이득은
A v = 4 × 25 = 100 A_v=4\times25=100 A v = 4 × 25 = 100 이다. 이를 dB로 표현하면
A v ( d B ) = 20 l o g 100 = 40 A_v(dB)=20log 100=40 A v ( d B ) = 20 l o g 100 = 40 이므로 답은 3번 이다.
12번 T 2 T_2 T 2 Q 2 Q_2 Q 2 T 3 T_3 T 3 Q 1 Q_1 Q 1 4번 이다.
13번 그렇다. 그렇지 않다. 불순물 도핑 농도가 높을수록 정공의 수가 증가하므로 저항률이 감소한다. 그렇다. 옥텟 규칙을 만족하기 위해서 이웃들과 4개씩 공유결합을 해야하는데 최외각 전자가 3개면 하나가 부족하다. 이 하나의 빈 자리가 정공이다. 그렇다. 그만큼 최고 에너지준위에 전자가 있을 확률이 높은 것이다. 따라서 답은 2번 이다.
14번 R C R_C R C 3번 이다.
15번 -단에 걸리는 전압은 3 4 V o \frac{3}{4}V_o 4 3 V o A = 3 A=3 A = 3
V o = 3 ( V i − 3 4 V o ) ⇒ 3 V i = 13 4 V o ⇒ V o V i = 12 13 \begin{equation} \begin{split} V_o&=3\left(V_i-\frac{3}{4}V_o\right)\\ \Rightarrow 3V_i&=\frac{13}{4}V_o\\ \Rightarrow \frac{V_o}{V_i}&=\frac{12}{13} \end{split} \end{equation} V o ⇒ 3 V i ⇒ V i V o = 3 ( V i − 4 3 V o ) = 4 13 V o = 13 12 이므로 답은 3번 이다.
16번 베이스 전압은
V B = 10 × 2.2 2.2 + 10 ≈ 1.7 V \begin{equation} \begin{split} V_B&=10\times\frac{2.2}{2.2+10}\\ &\approx 1.7\text{ V} \end{split} \end{equation} V B = 10 × 2.2 + 10 2.2 ≈ 1.7 V 이다. 따라서 이미터 전압은 V E = 1 V V_E=1\text{ V} V E = 1 V
I E = I C = 1 1 = 1 mA \begin{equation} \begin{split} I_E&=I_C\\ &=\frac{1}{1}\\ &=1\text{ mA} \end{split} \end{equation} I E = I C = 1 1 = 1 mA 이다. 따라서 컬렉터 전압은
V C = 10 − 3.6 = 6.4 V V_C=10-3.6=6.4\text{ V} V C = 10 − 3.6 = 6.4 V 이다.(오타 알려주신 통신해보자님 감사합니다.) 그러므로
V C E = 5.4 V_{CE}=5.4 V CE = 5.4 이다. 이와 가장 가까운 값은 2번 이다.
17번 실횻값은 반파나 전파나 같다. 제곱해서 평균낸 후 제곱근을 취하기 때문이다. 따라서 I o ( r m s ) = 220 10 A I_{o(rms)}=\frac{220}{10}\text{ A} I o ( r m s ) = 10 220 A V o V_o V o 1 π ∫ 0 π 2 × 220 × s i n θ d θ = 2 × 220 π × 2 \frac{1}{\pi}\int_0 ^\pi \sqrt{2}\times 220 \times sin\theta d\theta=\frac{\sqrt{2}\times220}{\pi}\times 2 π 1 ∫ 0 π 2 × 220 × s in θ d θ = π 2 × 220 × 2 전파 정류가 되므로 주파수는 2배가 된다. D 1 D_1 D 1 D 2 D_2 D 2 2 × 220 \sqrt{2}\times 220 2 × 220 2 × 220 − 0 = 2 × 220 \sqrt{2}\times 220-0=\sqrt{2}\times 220 2 × 220 − 0 = 2 × 220 따라서 답은 2번 이다.
18번 g m = I c V T g_m=\frac{I_c}{V_T} g m = V T I c 이다. 입력이 0일 때,
I R E = − 0.7 + 10.7 20 = 0.5 mA I_{R_E}=\frac{-0.7+10.7}{20}=0.5\text{ mA} I R E = 20 − 0.7 + 10.7 = 0.5 mA 이다. 이 전류는 양쪽 이미터에서 똑같이 왔으므로 Q 1 Q_1 Q 1
g m 1 = 0.25 26 = 1 104 g_{m1}=\frac{0.25}{26}=\frac{1}{104} g m 1 = 26 0.25 = 104 1 이다. 따라서 Q 1 Q_1 Q 1
I E 1 = g m 1 V i = V i 104 mA I_{E_1}=g_{m1}V_i=\frac{V_i}{104} \text{ mA} I E 1 = g m 1 V i = 104 V i mA 이다. 만약 Q 2 Q_2 Q 2 Q 2 Q_2 Q 2 20 × 52 104 = 10 V 20\times\frac{52}{104}=10\text{ V} 20 × 104 52 = 10 V Q 2 Q_2 Q 2 5 V 5 \text{ V} 5 V 1번 이다.
19번 직접
R S + j ω L 1 ∣ ∣ 1 j ω C 1 R_S+j\omega L_1 \left|\left| \frac{1}{j\omega C_1}\right.\right. R S + jω L 1 ∣ ∣ ∣ ∣ jω C 1 1 을 풀 수도 있겠으나 그러고 싶진 않다.
주파수가 0이면 등가 임피던스는 R S R_S R S R S R_S R S Ω \Omega Ω ω L 1 \omega L_1 ω L 1 C 1 ω C_1\omega C 1 ω 2번 임이 확실해졌다.
20번 Y ( s ) = H ( s ) ( X ( s ) − β Y ( s ) ) ⇒ Y ( s ) ( 1 + β H ( s ) ) = H ( s ) X ( s ) ⇒ Y ( s ) X ( s ) = H ( s ) 1 + β H ( s ) = A 0 ( 1 + s ) ( 1 + s 3 ) 1 + β A 0 ( 1 + s ) ( 1 + s 3 ) = A 0 ( 1 + s ) ( 1 + s 3 ) + β A 0 = A 0 ( 1 + s ) ( 1 + s 3 ) + 1 3 = A 0 1 + 4 3 s + s 2 3 + 1 3 = 3 A 0 s 2 + 4 s + 4 = 3 A 0 ( s + 2 ) 2 \begin{equation} \begin{split} Y(s)&=H(s)(X(s)-\beta Y(s))\\ \Rightarrow Y(s)(1+\beta H(s))&=H(s)X(s)\\ \Rightarrow \frac{Y(s)}{X(s)}&=\frac{H(s)}{1+\beta H(s)}\\ &=\frac{\frac{A_0}{(1+s)\left(1+\frac{s}{3}\right)}}{1+\frac{\beta A_0}{(1+s)\left(1+\frac{s}{3}\right)}}\\ &=\frac{A_0}{(1+s)\left(1+\frac{s}{3}\right)+\beta A_0}\\ &=\frac{A_0}{(1+s)\left(1+\frac{s}{3}\right)+\frac{1}{3}}\\ &=\frac{A_0}{1+\frac{4}{3}s+\frac{s^2}{3}+\frac{1}{3}}\\ &=\frac{3A_0}{s^2+4s+4}\\ &=\frac{3A_0}{(s+2)^2} \end{split} \end{equation} Y ( s ) ⇒ Y ( s ) ( 1 + β H ( s )) ⇒ X ( s ) Y ( s ) = H ( s ) ( X ( s ) − β Y ( s )) = H ( s ) X ( s ) = 1 + β H ( s ) H ( s ) = 1 + ( 1 + s ) ( 1 + 3 s ) β A 0 ( 1 + s ) ( 1 + 3 s ) A 0 = ( 1 + s ) ( 1 + 3 s ) + β A 0 A 0 = ( 1 + s ) ( 1 + 3 s ) + 3 1 A 0 = 1 + 3 4 s + 3 s 2 + 3 1 A 0 = s 2 + 4 s + 4 3 A 0 = ( s + 2 ) 2 3 A 0 이므로 극점은 s 1 = s 2 = − 2 s_1=s_2=-2 s 1 = s 2 = − 2 4번 이다.
21번 R E = 2.4 2 = 1.2 k Ω R_E=\frac{2.4}{2}=1.2\text{ k}\Omega R E = 2 2.4 = 1.2 k Ω 이다. 그리고 V C E Q = 5.2 V V_{CEQ}=5.2\text{ V} V CEQ = 5.2 V V C = 7.6 V V_C=7.6\text{ V} V C = 7.6 V
R C = 10 − 7.6 2 = 1.2 k Ω R_C=\frac{10-7.6}{2}=1.2\text{ k}\Omega R C = 2 10 − 7.6 = 1.2 k Ω 이므로 답은 1번 이다.
22번 카르노 맵을 만들면
A B C D 00 01 11 10 00 0 1 1 1 01 0 0 0 1 11 0 0 1 1 10 0 0 1 1 \begin{array}{c|c|c|c|c} ABCD & 00 & 01 & 11 & 10 \\ \hline 00 & 0 & 1 & 1 & 1 \\ \hline 01 & 0 & 0 & 0 & 1 \\ \hline 11 & 0 & 0 & 1 & 1 \\ \hline 10 & 0 & 0 & 1 & 1 \\ \hline \end{array} A BC D 00 01 11 10 00 0 0 0 0 01 1 0 0 0 11 1 0 1 1 10 1 1 1 1 이므로
F = A ‾ ⋅ B ‾ D + C D ‾ + A C F=\overline{A}\cdot\overline{B}D+C\overline{D}+AC F = A ⋅ B D + C D + A C 이다. C로 묶으면 A + D ‾ A+\overline{D} A + D
(가) ‾ + (나) ‾ = A + D ‾ \overline{\text{(가)}}+\overline{\text{(나)}}=A+\overline{D} ( 가 ) + ( 나 ) = A + D 이다. 그러므로 하나는 A ‾ \overline{A} A D D D 1번 이다.
23번 R 1 R_1 R 1 0.7 + 0.7 = 1.4 V 0.7+0.7=1.4\text{ V} 0.7 + 0.7 = 1.4 V
V o = 5 + 1.4 = 6.4 V V_o=5+1.4=6.4\text{ V} V o = 5 + 1.4 = 6.4 V 이다.
따라서
I s = 10 − 6.4 2 = 1.8 mA I_s=\frac{10-6.4}{2}=1.8\text{ mA} I s = 2 10 − 6.4 = 1.8 mA 이므로 답은 4번 이다.
24번 C = 1 C=1 C = 1 Q = X Q=X Q = X C = 0 C=0 C = 0 Q Q Q 1번 이다.
25번 차단 주파수는 1 2 π R A C A = 1 π \frac{1}{2\pi R_AC_A}=\frac{1}{\pi} 2 π R A C A 1 = π 1
V i = V o R 2 R 1 + R 2 ⇒ A v = V o V i = 1 + R 1 R 2 = 1.586 \begin{equation} \begin{split} V_i&=V_o\frac{R_2}{R_1+R_2}\\ \Rightarrow A_v&=\frac{V_o}{V_i}\\ &=1+\frac{R_1}{R_2}\\ &=1.586 \end{split} \end{equation} V i ⇒ A v = V o R 1 + R 2 R 2 = V i V o = 1 + R 2 R 1 = 1.586 이다. 따라서 답은 1번 이다.
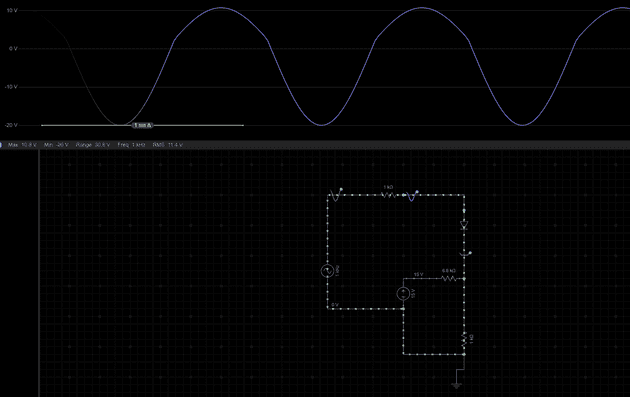(정정을 도와주신 중관소 꿈나무님께 감사드립니다.)
식을 세우자.